極限問題
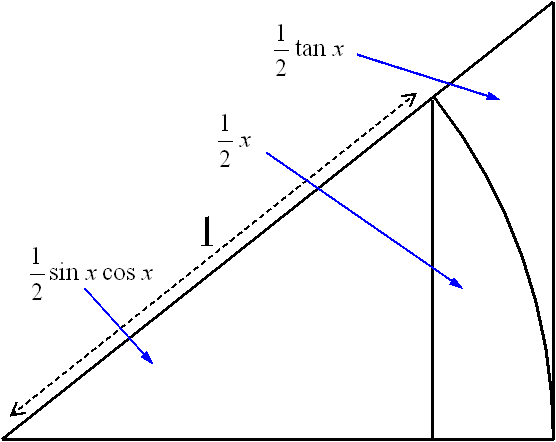
弧度法を面積で定義すると、以下の図で、角度xの円弧をはさむ二つの三角の面積関係から、
sinx cosx < x < tanx
となり、
cosx < (sinx / x ) < 1/cosx
より、
![]()
が証明できます。
三角関数の微分
弧度法の定義
微分では角度に弧度法(ラジアン)を利用しますが、実はこの定義法が重要です。ここでは、半径rの弧の面積をSとすると、中心角を 2S/r2 とします。
cos x の微分
sin x とどうように
(cos x)' = -sin x
を導くことができます。
参考http://ufcpp.net/study/miscmath/lopital.html
極限問題
弧度法を面積で定義すると、以下の図で、角度xの円弧をはさむ二つの三角の面積関係から、
sinx cosx < x < tanx
となり、
cosx < (sinx / x ) < 1/cosx
より、
![]()
が証明できます。
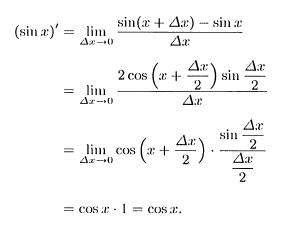
sin(x)の微分
以下のように導くことができます。