再帰処理

再帰処理とは
　コンピュータの繰り返し処理は、単純？な作業の繰り返しで、根気さえあれば真似ができそうです。しかし、一見単純な繰り返しなのに、複雑な作業に見える処理がここで紹介する「再帰処理」です。
再帰的な定義
　ある物を定義するとき、定義したい「物」を利用して定義する場合があります。これを再起的な定義と呼びます。たとえば、階乗の計算は以下のように再帰的に定義されます。n! の定義に (n-1)! を利用しているところが「再帰的」です。
```
　n!
　 =1　　       : n=0
　 =n * (n-1)!　: n>0
```
これで，すべてのnに対する fact(n) の値が求められます．たとえば
　2! = 2 * 1!= 2 * 1 * 0! = 2*1*1 = 2
n! をメソッドの fact(n) に置き換えると、次のようになります。
```
　fact(n)
　 =1　　          : n=0
　 =n * fact(n-1)　: n>0
```
　これは、そのまま、次のように計算できます。
```
//階乗の計算
void setup() {
  println(fact(10));
}

long fact(long n) {
  if (n == 0) return(1);
  else {
    return n*fact(n-1);
  }
}
///結果
3628800
```
　一見、どこにも繰り返しはありませんが、実は呼び出しの「連鎖」が起こっています。fact(10) は fact(9)の計算を必要とします。したがって、fact(10) につづけて fact(9) の呼び出しが起こります。どうように、fact(8)、..、fact(0) まで連鎖が起こり、fact(0) の呼び出しになります。これは、1 で戻るため、fact(1)が求められ、..、でfact(9)まで戻ると、10*fact(9) が決定し終了します。繰り返しは、コンピュータの中では呼び出しの連鎖となっています。

ハノイの塔の問題

　この再帰も、次の問題になると、立派な？パズルになります。

５枚の大きさの異なる円盤を順に重ねた塔Aがある。
この塔Aの円盤を塔Bに次のルールにしたがって移せ。
　ルール１：他の塔Cを移動作業用に利用できるが、それ以外の場所に円盤を置くことはできない．
　ルール２：小さな円盤の上に大きな円盤を置くことはできない．

この問題は次のように再帰的に解くことができます。

1枚の移動は簡単にできます。
一般にｎ枚の塔を最初の n-1 と最後の1枚に分割します。
 S1: 上の nｰ1 枚の塔を B を利用してして A から C に移動する
 S2: 最後の n 枚目の円盤を A から B に移す
 S3: C にある nｰ1 枚の塔を A を利用して C から B に移す

　n 枚の塔の移動を n-1 枚の塔の移動に帰着させています。「4枚ができれば5枚はできる」の論理です。4枚は、3,2,1 枚ができればよいから、「5枚」も”できるはず”です。
　といっても、簡単には手順にならないですよね。
　Processingで書いてみます。hanoi(nod,'A','B','C'); は　「nod 枚を A　から B まで C を経由して運ぶ手続きを表示する」メソッドです。この中で、num-1 枚を実行するする hanoi(num-1, A, C, B);　と hanoi(num-1, C, B, A); を呼び出します。実際の手続きの表示は、中間の println() の中にあります。

// hanoi
int nod;
boolean waitf;
void setup(){
  nod=5;
  waitf=true;
  hanoi(nod,'A','B','C');
}

void draw(){  
}

void hanoi(int num,char A,char B,char C)
{
 if ( num > 0){
   //Numｰ1枚の円盤をBを利用してAからCへ移動  
   hanoi(num-1, A, C, B);
   //移動メッセージ 
   println("move "+num+" th disk from " + A + " to "+B);
   waitf=true;
   //Num枚目（最も大きな円盤をAからBに移動する)
   hanoi(num-1, C, B, A); //Numｰ1枚の円盤をAを利用してCからBへ移動
 }
}

これで、一瞬のうちに以下のような「解答マニュアル（31回の移動）」がでてきます。一般に n枚の塔の移動に 2 の n乗 -1 の手数が必要です。

move 1 th disk from A to B
move 2 th disk from A to C
move 1 th disk from B to C
move 3 th disk from A to B
move 1 th disk from C to A
move 2 th disk from C to B
move 1 th disk from A to B
move 4 th disk from A to C
move 1 th disk from B to C
move 2 th disk from B to A
move 1 th disk from C to A
move 3 th disk from B to C
move 1 th disk from A to B
move 2 th disk from A to C
move 1 th disk from B to C
move 5 th disk from A to B
move 1 th disk from C to A
move 2 th disk from C to B
move 1 th disk from A to B
move 3 th disk from C to A
move 1 th disk from B to C
move 2 th disk from B to A
move 1 th disk from C to A
move 4 th disk from C to B
move 1 th disk from A to B
move 2 th disk from A to C
move 1 th disk from B to C
move 3 th disk from A to B
move 1 th disk from C to A
move 2 th disk from C to B
move 1 th disk from A to B

再帰図形

　こんな図形はいかがでしょうか？　Sierpinsky の再帰図形です。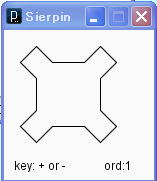

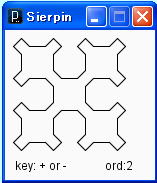
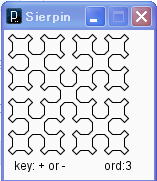
　n次の Sierpinsky の図　s(n) は、n次の図形 A、B、C、D、から定義されます。n次の図形Aを描画するメソッドが da(n)、B,C,D のそれが db(n)、dc(n)、dd(n) とします。da(n) は、da(n-1)、db(n-1)、dd(n-1)、da(n-1)とその間を接続する長さ h の線分で再帰的に定義されます。

//シェルピンスキー図形
int x, y, h, i;
int x0, y0;
int px, py, cx, cy;
int order;
int h0;
void setup() {

  size(300, 300);
  h0=512;
  cx=0;
  cy=-h0/2;
  smooth();
  order=4;
}

void draw() {
  background(250);
  fill(0);
  text("key: + or -",10,height-10);
  text("ord:"+order,100,height-10);
 

  h=h0/4;
  x0=2*h;
  y0=3*h;

  for (i=0;i<=order;i++) {
    x0=x0-h;
    h=h/2;
    y0=y0+h;
    if (i==order) {
      x=x0;
      y=y0;
      setplot();
      da(i);
      x +=h;
      y -=h;
      plot();
      db(i);
      x -=h;
      y -=h;
      plot();
      dc(i);
      x -=h;
      y +=h;
      plot();
      dd(i);
      x +=h;
      y +=h;
      plot();
    }
  }
}


public void setplot() {
  px=x;
  py=y;
}

public void plot() {

  line(px+cx, py+cy, x+cx, y+cy);
  px=x;
  py=y;
  //System.out.println("x:"+x+" y:"+y);
}

public void da(int i) {
  if (i>0) {
    da(i-1);
    x +=h;
    y -=h;
    plot();
    db(i-1);
    x +=2*h;
    plot();
    dd(i-1);
    x +=h;
    y +=h;
    plot();
    da(i-1);
  }
}

public void db(int i) {
  if (i>0) {
    db(i-1);
    x -=h;
    y -=h;
    plot();
    dc(i-1);
    y -=2*h;
    plot();
    da(i-1);
    x +=h;
    y -=h;
    plot();
    db(i-1);
  }
}

public void dc(int i) {
  if (i>0) {
    dc(i-1);
    x -=h;
    y +=h;
    plot();
    dd(i-1);
    x -=2*h;
    plot();
    db(i-1);
    x -=h;
    y -=h;
    plot();
    dc(i-1);
  }
}

public void dd(int i) {
  if (i>0) {
    dd(i-1);
    x +=h;
    y +=h;
    plot();
    da(i-1);
    y +=2*h;
    plot();
    dc(i-1);
    x -=h;
    y +=h;
    plot();
    dd(i-1);
  }
}

//キー入力で order 変更
void keyPressed() {
  if(key == '+' || key==';') {
    order++;
    if(order>6) order=6;
   
  } else if(key == '-') {
    order--;
    if(order<1) order=1;
  }
  println(order);
  repaint();
}

発展

再帰処理

再帰処理とは

再帰的な定義

ハノイの塔の問題

再帰図形

発展