倒立振子

参考文献
　この内容の制御理論は、
雨宮：「機械制御入門」　オーム社
　を参考にいたしました。
倒立振子
1. 倒立振子とは
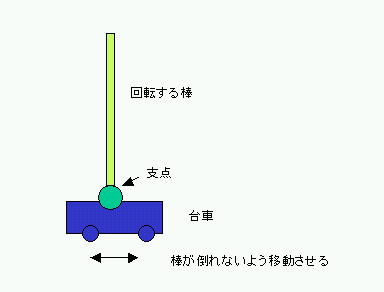
  倒立振り子は「棒振り子」を回転する側を下にし、その支点を左右に移動可能な台車に設置したモデルです。
  この振り子を垂直にしても、ちょっとした外乱で倒れてしまいます。台車を左右に移動することで、この振り子を倒れないように制御をすることが目的です。
2. 制御理論
  　モデルが数学的に定義できる場合、安定状態を維持する制御手法は古典的制御理論と呼ばれ、広く応用されています。
  　システムの状態がいくつかの変数 x = (x1,x2,..xn) で表現される場合、その時間変化は、
  
  　　dx/dt =A・x
  
  で、数学的に表現されるとします。A はn*n の行列です。システムがこのままでは安定にならない場合、外部から u の力を加えます（これが外部からの制御になります）。このときシステムの時間変化は
  
  　dx/dt =A・x + B・u
  
  となります。一般に u は、u = K・ x と、状態変数をK倍した値とします。。この場合、
  
  　dx/dt =A・x + B・K・x = （ A　+ B・K ）・x
  
  となります。（ A　+ B・K ）が、一定の条件を満たしていると、時間と共に x の値を 0 となるよう、K の値を定めることができます。ここで、K は x と同じ次数の定数ベクタです。
  　
3. 運動方程式
  　A,B は運動方程式から定まります。
  振り子の質量を m、重心からの長さを L、慣性モーメントを I とします。また、台車の質量を M とします。
  台車に加える外力（水平方向）を u 、振り子の支点に働く水平方向の力を H,垂直上方向の力を V とします。
  また、振り子の垂直方向からの傾きを φ、支点の水平方向の位置を x とします。
  
  　まず、支点周りの回転に関する運動方程式は
  
  　
  
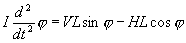
  となります。また、振り子の x,y 方向の運動方程式は次のようになります。
  
  　
  
  　
  
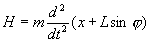
  台車に関する、x方向の運動方程式は次のようになります。台車の y 方向の運動は、床との反力なので、摩擦を考える場合必要ですがここでは考慮しません。
  
  　
  
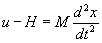
  このままでは、簡単には解けませんから、三角関数の線形化をします。φの値が小さいとき、
  　sin φ= φ　cos φ = 1
  と、近似できます。この近似を利用すると、上の式は次のようになります。
  
  　
  
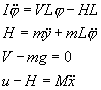
  この式から、H、V を消去すると、次のようになります。
  
  　
  
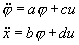
  ここで、a,b,c,dは以下のような定数になります。
  
  　
  
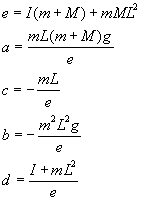
  I は、同じ太さの棒の場合、
  
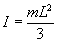
  となります。
4. 状態方程式
  運動方程式を、状態方程式に変形します。
  
  を状態変数にします。これで、
  
  　
  
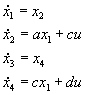
  となり、状態方程式の形になります。ここで
  
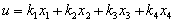
  として、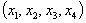が安定解をもつよう、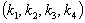を求める必要があります。
5. 極配置法による解
  　安定解を求める方法の一つに、極配置法があります。これは、予め、状態方程式の特性根（固有値）を安定解が得られるよう設定し、その特性根から、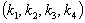を定める方式です。
  　特性根を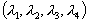　と
  と定めます。実部が負になるよう設定する必要があります。これから、特性方程式の係数比較で以下の連立方程式が導かれます。
  
  　
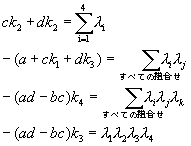
6. 数値例
  m=0.3kg、L=0.6m、M=0.6kg としますと、I=0.036、a=16.3、b=-3.2、c=-1.8、d=1.6　となります。
  
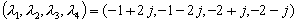
  とすると、
  
  　k1=19.6、 k2=4.56、k3=1.37、k4=1.65
  
  となります。
7. 　シミュレーション
  　これで、シミュレーションの準備ができました。
  シミュレーションは、まず、各状態の初期値を設定します。
  次に、短い時間間隔で状態方程式を利用して、次ぎの時刻の状態の値を求めます。
  これをくりかえして、安定状態（状態変数が0になる）に入るまでの変化を調べます。
  
  具体的には、
  
  　x1=0.1, x2=x3=x4=0.0
  
  を初期状態とします。x1は棒の傾きですから、棒が少し傾いた状態です。
  
  　
  
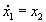
  は、x1' を　x1 の dt 後の値とすると、(x1' - x1)/dt = x2 の意味ですから、
  
  　x1' = x1 + x2・dt
  
  としてもとめることができます。どうように、
  
  から、
  　x2' = x2 + (a・x1 + c・u )dt
  
  となります。x3'、x4' も求めます。これで、dt 時刻後の各状態の値が求まったことになります。
  
  　x1 = x1' ,x2 = x2' ,x3 = x3' ,x4 = x1' ,
  
  として、繰り返し計算を行います。dt = 0.01 とすると、100回の計算で1秒後の状態を計算することができます。
  
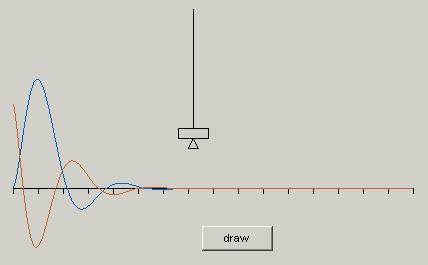
  下図赤線が角度の時間推移を示します。青線はx座標です。2回程度のオ-バーシュートで0点に収束しています。右側の図は、k1=16.0 に変更してシミュレーションしたものです。収束が遅くなります。
プロジェクト
1. プロジェクト
  Applet1クラスで、Thread を利用し、単位時間間隔で次ぎの状態の値を計算し、グラフと倒立振り子の簡易表示を行います。
  Stateクラスで、状態の設定と単位時刻後の計算を行います。
2. Applet1クラス
  　実時間の変化を表示するため、Treadを利用し、sleepをしながら表示をします。以下に、Treadのrun()を示します。Stateクラスで、振り子の状態を生成します。st.Next() で1時刻進め、グラフ表示のため、状態の角度と位置を配列 xp[] と ang[] にスケール変換して保存します。180時刻の試行で、打ち切ります。
```
public void run(){
    //スレッドによる時間進行

  boolean cont=true;
  st = new State();
  inum=0;
  while(cont){
    st.Next();//次に時刻の値
    xp[inum]=(int)(st.Xp*200.0);
    ang[inum]=(int)(st.Ang*1000.0);
    repaint();
    inum++;
    if(inum>=180) cont=false;

    try{
      Thread.sleep(100);
    }
    catch(Exception e){}
    }
    System.out.println("Thread out\n");
  }
```
  paint()でグラフ表示、drawPend()で振り子のアニメーションをします。三角印は原点を表示しています。
  
  ソースはこちらをご覧下さい。
3. StateRクラス
  　コンストラクタで、初期値を設定、next() で単位時刻（step）後の状態計算をします。以下に Next()関数を紹介します。まず、vu（外部からの力）を計算し、
  　Ang, dAng, Xp, dXp が状態　x1,x2,x3,x4 に対応します。
```
  public void Next() {
    //次の時刻の値を求める
    double vu;
    vu = ck1 * Ang + ck2 * dAng + ck3 * Xp + ck4 * dXp;

    ddAng = ca * Ang + cc * vu;
    dAng += ddAng * step;
    Ang += dAng * step;

    ddXp = cb * Ang + cd * vu;
    dXp += ddXp * step;
    Xp += dXp * step;

    Time += step;
  }
```
  ソースはこちらをご覧下さい。
4. Complexクラス
  　複素数のクラスです。複素数の定義、加算、乗算演算を定義します。
  ソースはこちらをご覧下さい。
5. 実行
  　起動すると以下のような設定画面がでます（見えない場合、ブラウザの背面などに隠れています）。振り子（棒）の重さ（Kg）、重心からの長さ（単位M、同じ太さの棒なら、実長の半分）、台車の重さを設定します。棒の太さが同じで、錘りなどを付加していない場合、棒の回転モーメントは -1.0 とすると、理論値を計算します。正の値を指定すると、その値で計算します。振り子の先端に錘をつけた場合は、ここに値を設定します。
  
  　次に棒の初期角、位置を設定します。共に0にすると、まったく動きません。理論的に計算できる角度の範囲は10度程度です。単位時間は、シミュレーションを行うステップ時間を指定します。
  　ck1,..,ck4 は、台車を制御するフィードバックの割合を示します。実行すると、極配置法による計算値に置き換えます。正の値にすると、その値を使って計算をします。理論値に戻すには、-1を設定します。
  
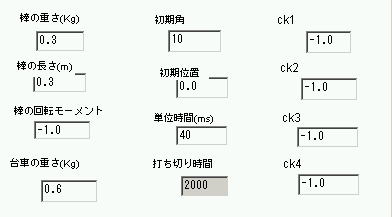
  draw ボタンを押すと、指定した初期角と初期位置からシミュレーションを開始します。角度と位置の時間変化をグラフで表示し、振り子の状態をアニメーションします。三角マークが原点の位置を示します。
  
  物理的な条件は変更しないで、ck1、..ck4 の値や、棒の回転モーメントを変化させると、振り子の動きがどうなるかをシミュレーションできます。ck1,ck2 の値を2割以上変えると、振り子の動きが増大することも確認できます。
実際の制御システム
1. PID制御
  　設定値と制御変数の差（偏差）、および、その微分値と積分値を用いて制御を行うのが、PID制御です。ここでは、偏差でなく、状態を用いていますが、状態には物理量の微分値も利用していますから、実質的には　PD 制御になります。
  　I 制御は、偏差が少なくなると制御量が減りオフセットは発生する現象を補完するための補助的な機能です。
2. 状態変数
  　この方法で制御するには、状態の値を知る必要があります。この例の場合、棒の角度φと位置xを取得する必要があります。
  また、微分値を計算し状態ベクトルとします。これに、フィードバック係数をかけてトルクを算出し、モータの制御を行います。
3. ディジタル制御
  ディジタル制御を行う場合、角度φと位置xをセンサーで取り出し、ディジタル変換します。
  状態の微分値は、前の状態からの差で推定できます。
  状態にフィードバック係数をかけて、外力（トルク）を求めます。
  モータ特性からこのトルクを生成する電流を求めて、モータに加えます。
  これを繰り返して制御を行います。