漸化式と再帰アルゴリズム

1. 線形漸化式

   
   

   1. ハノイの塔の移動回数

      ハノイの塔では、n 枚の塔の移動に、(n-1)枚の移動が2回必要でした。n 枚の移動に必要な移動回数を A(n ) とすると、
      
      　A(n) = A(n-1) + A(n-1)+ 1 = 2 * A(n-1)+1;　
      　
      となります。A(1)=１ ですから、A(2)=3、A(3)=7、..,　A（n)=2ⁿ-1 は比較的簡単に導くことができます。
      
      この式のように、A（n-i） で関係つけられた式を漸化式といいます。特に、
      
      　C₀A(n) + C₁A(n-1) + ..  + C_rA(n-r) = f(r)　　　
      
      の形になる漸化式を線形漸化式といいます。線形は、直線的に接続されている意味です。
      

   2. 演習

      A（n)=2ⁿ-1 を確認してください。
      
      

   3. 線形漸化式の解（フィボナッチ数列の場合）

      　線形の漸化式は一般解を求めることができます。フィボナッチ数列の第 n 項の値を　A(n) とします。このとき、
      　
      　　A(n) = A(n-1) + A(n-2)　　　
      
      となります。これは、線形の漸化式です。ハノイの塔の類推で A(n) = αⁿ と考えます。これを、代入すると、
      
      　αⁿ - α^n-1 - α^n-2 = 0　　
      
      となります。αは0でないものとして α^n-2 で割り算すると、
      
      　α² - α - 1= 0  
      
      となります。この式を特性方程式と呼びます。これを解くと、
      
      　α₁= （1 + √5）/2　、α₂= （1 - √5）/2
      
      となります。この二つが解ですから、一般に、
      
      　A(n) = c₁ α₁ⁿ + c₂ α₂ⁿ
      
      となりそうです。ここで、n = １,2  の場合を代入すると
      
      　A(1) = c₁ α₁  + c₂ α₂= 1
        A(2) = c₁ α₁² + c₂ α₂² = 1
      
      となります。α₁  と　α₂ は定数ですから、c1, c2 を連立方程式として解くことができます。結果、
      
      
      
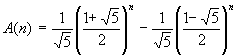
      となります。√ がでてきて一瞬ギョッとしますが、ためしにA(１)やA（2) を計算してみてください。答えは整数になります。
      
      

   4. 演習

      　A(2), A(3) の場合を計算して下さい。
      　また、Excel か プログラムで、r = 10までの値を計算してください。
      
      

   5. 一般の場合

      　一般には、特性方程式が重根（2次方程式が同じ根をもつ）であったり、漸化式の左辺が0でなく
      
      　　C₀A(n) - C₁A(n-1) + C₂A(n-2) = f(n)　　　
      
       のように、n の多項式になる場合も一般解が存在しますが、詳細は省略します。
      　C.L.リュ-著　　「離散数学入門」
      には詳細な解法があります。
      
      

2. 線形でない漸化式

   
   

   1. 線形でない漸化式（二分探索）

      　大きさの順に並んだデータを検索するとき、2分探索を用います。二分探索はデータの中央の値をしらべ、調べたいキーの値により、検査範囲を半分に限定できます。したがって、n 個のデータを検索するときの回数を A(n) とすると
      
      　A(n) = 1 + A( n/2)  
      
      となります。この解は
      
      　A(n) = log ₂ n
      
      となります。2 ¹⁰ = 1024　ですから、約千個のデータを10回でさがすことができます。
      
      ■
      x  = log _a b 　とすると、 　a ^x = b の関係があります。log (x /y ) =  log x / log y
      ですから log ₂ (n/2) は　log ₂ n　- log ₂ 2 となります。したがって、　
      
      　log ₂ (n/2) = log ₂ n　- 1
      
      となります。
      
      

   2. 線形でない漸化式（マージソート）

      マージソートは　二つの n/2 個のソート済みのデータを n 回の操作で（小さいデータを先に出す）ことで、n 個のソートされたデータにすることができます。たとえば、
      　3,8,12,15
      と
      　5,7,14,16
      の数列で、小さいほうを先に出すと、
      　3,5,7,8,12,14,16
      となります。この方法を利用すると、n 個のデータをソートする手間は
      
      　A(n) = n + 2・ A(n/2)
      
      となります。右辺の　 2・ A(n/2)　が、n/2 個の二つのデータをソートする手間、n が二つのソート済みのデータをマージする手間になります。この解は
      
      　A(n) = n log ₂ n
      
      となります。クイックソートの場合は、左辺と右辺が平均的に等しくなりますから、やはり、
      
      　A(n)  〜　 n + 2・ A(n/2)
      
      となります。〜 は平均的に等しいの意味です。