多角形の面積

1. 多角形の面積

   
   

   1. 格子点上の多角形

      ここでは、多角形の頂点は格子状の点にあるものとします。この多角形の面積を求めるのが問題です。下図の場合適当に切り分けて面積を求めることができます。
      
      
      
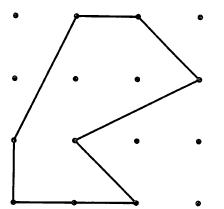
      下の場合、切り分けでなく、図と背景を逆転させる発想が必要です。全体の面積から、灰色の面積を減算します。
       　
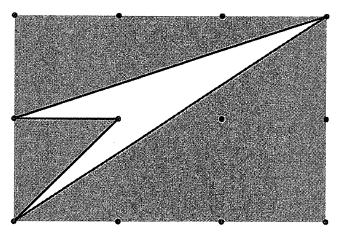
      ところで、一般に格子多角形の面積を求める面白い方法があることは、意外と知られていません。
      
      

   2. 演習

      上の二つの多角形の面積を求めてください。
      （ヒント：答えは　５ と １ です））
      
      

2. ピックの定理

   
   

   1. ピックの定理とは

      　一般的に格子多角形の面積に関する定理です。格子多角形内部の格子点の数を I とし、境界線状の格子点の数を B とします。このとき
      

      格子多角形の面積 S は S = I + B/2 - 1 に等しい

      というのがピックの定理です。ただし、格子多角形の境界線が自分自身と交わらないものとします。
      
      

   2. 演習

      　先の二つの例で、ピックの定理を確認して下さい。
      
      

   3. ピックの定理の加法性

      　ピックの定理を証明するには、ピックの定理の「加法性」を証明することが必要です。二つの多角形を複合した多角形の面積は、各多角形の和になります。ピックの式が面積となるには、この加法性が必要です。一般には、二つの多角形が共有する辺上の格子点の数は不明です。この数を k とします。また、左右の共有されない格子点の数を、IL と IR とします。
      　すると、複合図形の内点の数は　
      

       I　= IL + IR + k 

      となります。また、境界上の格子点の数を、BL、BR とします。すると、複合多角形の境界点の数 B は共有されている辺の数が余分ですから、
      

       B = BR - k + BL - k - 2

      となります。-2 は　共有される辺の両端の点の数です。したがって、ピックの定理による面積は、
      　S = I + B/2 - 1 = IL + IR + k + (BR - k + BL - k - 2)/2 -1 =  IL + IR + BL/2 + BR/2 -2= (IL + BL/2 -1) +( IR +BR/2 -1)
      となります。これは、二つの多角形のピックの定理の数の和になります。
      
      
      
      

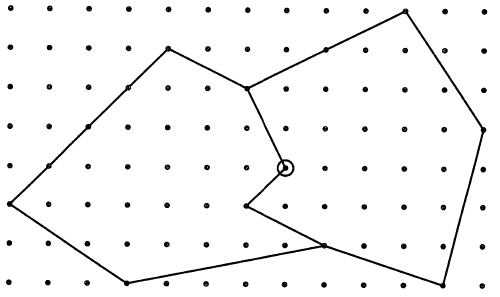
   4. 演習

      　上の図形で、左右の多角形の数と複合した多角形のピックの数を求めてください。
      
      

   5. 多角形の面積

      　加法性が証明できると一般図形の面積の証明が容易になります。境界線が交差しない多角形は複数の三角形に分解できます。したがって、任意の三角形の面積が　「ピックの数」 に等しくなれば、定理が証明できます。
      　これを、証明するには、まず、長方形の面積がピック数に等しいことを証明します。次に、長方形を二つに分割した直角三角形の面積がピック数に等しいことを証明します。幅ｗ、長さhの長方形（点の数はw + 1とh + 1）の内点の数は (h-1)*(w-1)になります。境界線上の点の数は、2w+ 2 +2h-2 ですから、ピック数は hw になります。三角形の面積はこの半分です。
      
      
      
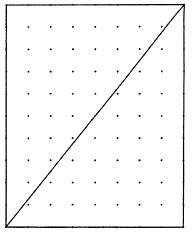
      最後に、任意の三角形の面積が長方形と直角三角形から計算できることを示します。
      
      
      

   6. 演習

      　辺の数が５以上の多角形を描き、面積がピック数に等しいことを確認してください。
      
      

   7. 参考文献

      このテキストの図は、下記の文献から引用させていただきました。
      キース・ボール著　「フォボナッチのうさぎ」　青土社