カタラン数


  1. カタラン数とは

    カタラン数は組み合わせの数として時々表れる数です。括弧のつけ方、多角形の分割、2点間の格子状の経路の数などの数え上げにカタラン数が登場します。

  2. 括弧のつけ方


    1. 括弧のつけかた

      まず、括弧のつかかたの数について考えます。2対の括弧の場合、( ) ( )と (( ))　で二通りです。3組の場合、
      　()()(), ()(()), (())(), (()()), ((())) の5通りです。

    2. カタラン数

      n組のかっこのつけ方を Cn と標記しカタラン数と呼びます。この数列は、19世紀のベルギーの数学者　オイゲネ・カタランが ｎ角形を三角形に分割する方法として発見しました。
      　C0=1、C1=1、C2=2、C3=5、となります。

  3. 再帰的関係式


    1. 再帰的関係

      　4組の括弧の場合を考えます。先頭に、( ) をつけると、残りは3組になります。
      　()()()(), ()()(()), ()(())(), ()(()()), ()((()))
      これを、 （）｛3組｝ と表現します。この組み合わせの数は3です。
      です。次に、最初の () の中に、もう一組の括弧が入っている場合を考えます。残りは2組ですから、これは次のように表現できます。
      　（{１組}）｛2組｝
      この組み合わせの数は、C1*C2 になります。どうように、
      　（｛2組｝）{１組}　や
      （｛３組｝）があります。これらを、寄せ集めると、
      　C4 = C3 + C1*C2 + C2 * C1 + C3　= 5+2+2+5 =14
      となります。C0=1 とする
      　Cn = Σ(i=0..n) Ci * C(n-i)
      となります。
      これが、Cn の再帰的定義になります。

    2. C5の計算

      この再帰式で、C５を計算します。
      第一行にC０からC４をならべ、2行に逆順に並べます。1行と2行をかけながら加えます。
        1 1 2 5 14
 14 5 2 1  1
      ですから、14+5+4+5+14 =42 となります。

  4. 経路の数(推測)


    1. 組み合わせ数による評価

      カタラン数は再帰ではなく、組み合わせ数で直接評価できます。このためには、経路数を評価するのが近道です。

    2. 格子状の経路の数

      格子状で左下から右上に行く経路を考えます。右をE、上をNで表します。すると、下の経路は NNENENEE になります。Nを左括弧、Eを右括弧に対応させると、これは、(( ）( ))) になります。


      　以下の経路は ENEENEN ですが、 )())()( となり正しい括弧づけではありません。これは、右括弧が先行しているために起こります。


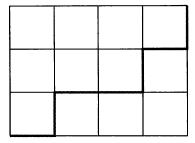
      左括弧が先行する場合、経路は数のように対角線より上の経路に限定されます。この対角線より上の経路の数が、カタラン数になります。


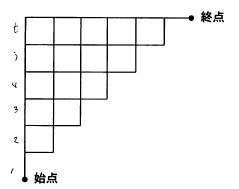
      n*n の格子上経路の数は、経路上の2n個の曲がり角で、n個の上（右）を選択する個数になりますから、2nCn です。これから、右下を通る場合の数を引けばよいことになります。ところで、Cn（カタラン数）と 2nCn を比較してみます。
      n Cn 2nCn 比
      ０ 1 1 1/1
      1 1 2 1/2
      2 6 6 1/3
      3 5 20 1/4
      4 14 70 1/5
      5 42 252 1/6

      二つの比率がきれいに1/nになっています。これで、
      　Cn = (1/(n+1)) 2nCn
      が予想できます。

  5. カタラン数（公式）


    1. 公式の証明

      　先に推測したカタラン数を証明します。ｎ行n列のすべての経路は 2nCn です。これから、対角線の右下に入る経路数を削除すれば、カタラン数になります。対角線ではなく、１経路右下に点線の斜め線を入れます。この斜め線上を通過する経路が削除対象です。この線にぶつかる最初の位置で経路を折り返します。すると、経路の最終点（n,n) も折り返され、(n+1,n-1)になります。
      　逆に、(n+1,n-1) に達する経路を点線を跨ぐ最初の点で逆に折り返せば、対角線の右下を通る経路になります。したがって、対角線の右下を通る曲線は (0,0) から (n+1,n-1) までの経路ですから、2nCn-1 になります。これで、
      　Cn = 2nC n − 2nCn-1 になります。

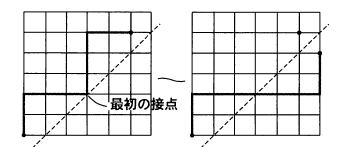
      他の経路の折り返しも同じです。
       

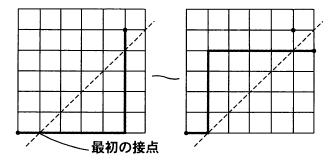
    2. 導出

      (n+1,n-1) に達する経路を点線を跨ぐ最初の点で逆に折り返せば、対角線の右下を通る経路になります。対角線の右下を通る曲線は、(0,0)から(n+1,n-1)までの経路ですから、2nCn-1 になります。これで、
      　Cn = 2nC n − 2nCn-1 になります。
      この式を、展開します。

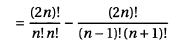
      です。分母を揃えて簡単化します。

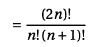
      となります。これは、 　Cn = (1/(n+1)) 2nCn と同じです。

    3. 計算

      これで、カタラン数の計算は簡単になります。2nCn から計算できます。
      n Cn
      1 1
      2 2
      3 5
      4 14
      5 42
      6 132
      7 429
      8 1430

    4. n! の近似式

      ここでは証明しませんが、n! に対して次の漸化式（スターリングの公式）が証明されています。

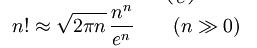
      漸化式は、n の値が大きくなると、真の値に近づく式のことです。これから、n! の値は、n が大きいとき (n/e) の n 乗に比例することがわかります。 したがって、カタラン数もどうようの評価が可能です。

  6. その他のカタラン数


    1. n個の和の順序

      n個の数の和を計算するとき、順序付けの数はCn-1になります。


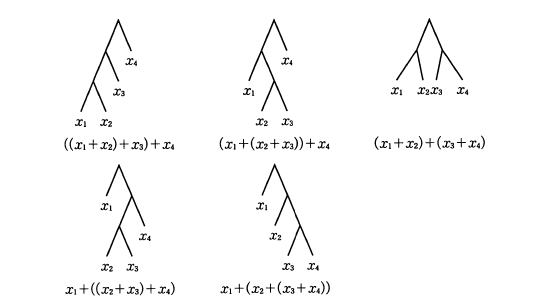
    2. 多角形分割

      凸n多角形を互いに交わらないように分割する方法は、Cn-2 になります。


    3. 2段に並べる

      　１から2nまでの整数を2段に並べます。このとき、右の数は左より大きい、下の数は上より大きいものとします。このときの並べ方はカタラン数Cnになります。


  7. 参考文献


    　仙波一郎　：組み合わせ数学
    　グロス：数のマジック
    　スターリングの近似式：Wikipedia