概要
カタラン数は組み合わせの数として時々表れる数です。括弧のつけ方、多角形の分割、2点間の格子状の経路の数などの数え上げにカタラン数が登場します。

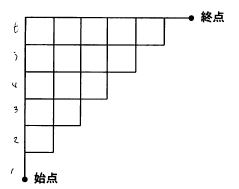
経路の数え上げ
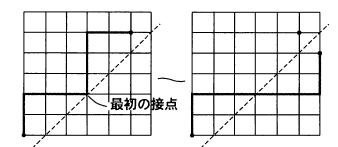
。ｎ行n列のすべての経路は _2nC_n です。これから、対角線の右下に入る経路数を削除すれば、カタラン数になります。対角線ではなく、１経路右下に点線の斜め線を入れます。この斜め線上を通過する経路が削除対象です。この線にぶつかる最初の位置で経路を折り返します。すると、経路の最終点（n,n) も折り返され、(n+1,n-1)になります。
　(n+1,n-1) に達する経路を点線を跨ぐ最初の点で逆に折り返せば、対角線の右下を通る経路になります。対角線の右下を通る曲線は、(0,0)から(n+1,n-1)までの経路ですから、_2nC_n-1 になります。これで、
　Cn = _2nC _n2 − _2nC_n-1 になります。

正しい括弧のつけ方
まず、括弧のつかかたの数について考えます。2対の括弧の場合、( ) と (( ))　で二通りです。3組の場合、
　()()(), ()(()), (())(), (()()), ((())) の5通りです。

再帰的関係
どうように、
　（｛2組｝）{１組}　や
（｛３組｝）があります。これらを、寄せ集めると、
　c4 = c3 + c1*c2 + c2 * c1 + c3　= 5+2+2+5 =14
となります。c0=1 を利用すると、
　cn = Σ(i=0..n) ci * c(n-i)
となります。

カタラン数

経路数
格子状で左下から右上に行く経路を考えます。右をE、上をNで表します。すると、下の経路は NNENENEE になります。Nを左括弧、Eを右括弧に対応させると、これは、((）())) になります。
左括弧が先行する場合、経路は数のように対角線より上の経路に限定されます。逆にこの経路の数が、カタラン数になります。

4組の場合
4組の括弧の場合を考えます。先頭に、( ) をつけると、残りは3組になります。
　()()()(), ()()(()), ()(())(), ()(()()), ()((()))
これを、 （）｛3組｝ と表現します。この組み合わせの数はC3です。
です。次に、最初の () の中に、もう一組の括弧が入っている場合を考えます。残りは2組ですから、これは次のように表現できます。
　（{１組}）｛2組｝
この組み合わせの数は、c1*c2 になります。

昇り優先の経路数
カタラン数は再帰ではなく、組み合わせ数でも評価できます。このためには、経路数を評価するのが近道です。