論理式の応用:加算回路
-
桁上がりのない加算回路
まず、桁上がりのない S = X+Y の1桁加算の表を作成しましょう。X,Y の値に対し、和:S は次のようになります。この演算は、OR演算と似ていますが、最後の行だけ違います。共に1のときはSは1にならないので、排他的論理和(EXclusive OR)とも呼ばれます。
X Y S 0 0 0 0 1 1 1 0 1 1 1 0
Sが1になるのは
X=0 かつ Y=1 、または X=1 かつ Y=0
となります。これを論理式で表現すると、
S = ^X ・Y + X ・^Yとなります。このように桁上がりを考慮しないで加算をする回路を 「半加算器:Half Adder」 ともいいます。半加算をここでは S = X ◎ Y であらわします。
問題1 スイッチ回路
この半加算回路は「 階段スイッチ」ににています。半加算を行うスイッチ回路を考えてください。
-
桁上がりを考慮した1桁加算回路
次に、桁上がりを考慮した1桁の加算回路を作成します。Cを前の段からの桁上がりとします。X,Y,C を入力とし、その和をSとすると下の表になります。X,Y,C を入力とし、その桁上げをDとする真理値表を作成します(空欄を埋めてください)
この表より S(和) と D(桁上がり) を計算する回路を作成することができす。
X Y C S D 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 1 1 0 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1
問題2
D の空欄を埋めてください。
-
半加算と全加算
Dは、X,Y,Cの二つ以上が1のとき1になります。したがって、
D = X・Y + X・C + Y・C
となります。
S も X,Y,C のAND,OR,NOTで計算できます。Sが1になるのは、(X,Y,C)が (0,0,1)、(0,1,0)、(1,0,0)、(1,1,1)の4種の場合です。これを論理式で表すと次のようになります。
S = ^X・^Y・C + X・^Y・C + X・^Y・^Z + X・Y・Z
排他的論理和を用いるともう少し簡単に表現できます。排他的論理和(EXOR)の記号を◎とします。S は X と Y の排他的論理和にさらにCを排他的論理和しますから、
S = X ◎ Y ◎ C
となります。排他的論理和は二つの信号の和を求めます。この桁上げを考慮した加算回路を 「全加算器」と呼ぶことがあります。
-
問題2
D の論理式を表から直接作成してください。
n桁の加算回路
-
n桁の2進数の加算
n桁の2進数の加算回路を表で定義することも可能ですが桁数が多くなると現実的でなくなります.例えば 5 桁の加算の場合入力数は10となりますから,表の行数は 1024 となってしまいます.
しかし,人は n桁の加算を一度に計算しているわけではありません。1 桁の計算を桁上げを通して繰り返すことにより計算しています.多桁の 2 進数の加算も 10 進と同様に 1 桁の加算の繰り返しで可能です。次に例を示します。桁上がりを考慮しながら、下位の桁から順に一桁づつ計算していく手順を確認して下さい(復習)。
0 0 1 0 + 0 1 1 0 ------------ 1 0 0 0
-
1桁の加算器を接続する
n桁の加算器は、一桁の加算器を次のように、縦続に接続して合成することができます。このとき、前桁の桁上げ出力Dを次の桁のC入力に接続します。最初の桁の桁上げ入力は0とします。この図をブロック図と呼びます。
出力Dは次の桁の入力Cとなります。このようにすると、1桁の回路ができればそれをn個並べるだけで、n桁の加算回路ができます。
-
問題3
n=3として次のように入力を定めたとき、各出力の値を図に記入してください。
(A3,A2,A1,A0)=(0,1,1,0)、 (B3,B2,B1,B0)=(1,0,1,0)
ドモルガンの定理
-
括弧式の否定は
^(A + B)のように、式や括弧の否定がある論理式の括弧をはずす方法を考えます。直感的には
^(A + B) = ^A + ^B ------(これは誤り)
と考えがちですが、これは誤りです。例えば、Aを1、Bを0としたとき左辺は ^( 1 + 0 ) = 0 ですが、右辺は ^1 + ^0 = 0 + 1 = 1 となります。
-
ド・モルガンの定理
論理式の最も重要な性質として、次のド・モルガン(De Morgan:人名)の定理を紹介します。否定のついた括弧をはずすには、このド・モルガンの定理を使います。括弧付の ^ の括弧をはずすと、論理和と論理積が入れ替わるという、一見とんでもないことがおこります。
^(A・B) = ^ A+^B ^(A+B) = ^A・^B
[証明1]
^(A・B) = ^ A+^B を証明します。
補元律より X・Y = 0 なら ^X = Y となります。X = A・B、Y =^ A + ^B として
(A・B) ・ (^A + ^B) = ( A・B・^A) + (A・B・^B) = 0
ですから、^(A・B) = (^A+^B) となります。
[証明2:代入法]
A=1 なら 左辺は ^B、右辺は 0 + ^B ですから成立します。
A=0 の場合、左辺は ^0 = 1、右辺は 1 + ^B = 1 となり、やはり、成立します。
この証明の方法を代入法と呼びます。
-
論理和と論理積は表と裏の関係
ド・モルガンの定理は論理和と論理積が独立ではなく、論理和は論理否定と論理積から計算できることを意味します。すなわち、ド・モルガンの公式の両辺の 論理否定 をとると
^(^(A・B)) = A ・ B = ^(^A + ^B)
となります。したがって、各項の論理否定をとってから論理和し、その結果を論理否定をすれば、結果は論理積と同じになります。
この性質は、論理演算の表からも確認できます。論理和はどちら一方が1のとき1になりますが、0を基本にすると、いずれも0のときだけ0となります。これは、0に関する論理積となります。
-
適用例
ド・モルガンの定理を用いて括弧をはずします。
^(A・B +B・^C) = ^(A・B)・^(B・^C) = (^A + ^B)・(^B + C)
= ^A .^B + ^A .C + ^B + ^B .C
-
問題4
次の 二つの式の( )をはずして、展開しなさい。
^(A + B + C)=
ヒント:x = A + B として、x + C を展開し、その後、x を展開します。
^(A + B・^C)=
注意:演算子の優先順位に注意して下さい。x = B ・ ^C として、まず、A + x を展開します。
減算回路(参考)
-
補数
減算を行うとき減算の専用回路を作成するのでなく、補数器を利用します。a の補数は a に加えると 0 になる数で10進数では -a に相当します。
-
2進数の補数
2進数の補数(正確には、2の補数)は、各桁の否定をとり、それに1を加えることで計算できます。たとえば 011 の補数は (111-011)+1 で計算できます。111からの引き算は各桁の否定で計算できます。先頭(一番左)ぼビットは符号ビットになります。
-
減算回路
減算回路 a - b は、bの各桁の否定と a を加え、さらに 1 を加えることで計算できます。最後の +1 は、最初の桁に桁上がりを加えることで計算できます。したがって、減算回路は次のように加算回路をちょっと変形するだけで作成できます。
引き算する信号の否定を加えます。
先頭の桁の桁上がり入力に1を加えます(これで +1 ができます)
(先頭の桁の桁上がりは、加算の場合は0とします)
-
減算回路のブロック図
以下に、減算回路のブロック図を示します。
-
演習問題2
01110 - 01101 の計算過程(各出力信号の値)を、上の図に書き込みなさい。
ゲート回路(参考)
-
ゲート素子の記号
NAD,OR,NOT の論理演算はディジタルIC(集積回路)を用いて作成できます。下図、左から、NOT、AND、OR 素子の記号です。
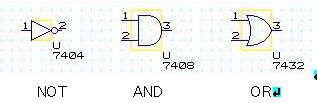
NOT、AND、OR 素子などをゲート素子と呼びます。
-
AND、OR、NOTの組み合わせ回路
すべての回路は(否定付きの)論理変数の論理積の和で表現されますから、NOT、AND、ORを組み合わせると任意の組み合わせ回路を合成することができます。
下図は A・^B + ^A・B の回路です。上のAND素子に、信号Aと信号BのNOTが入りますから、 A・^B を出力します。下のAND素子には、信号Bと信号AのNOTが入りますから ^A・B を出力します。これを OR したものが出力 D になります。
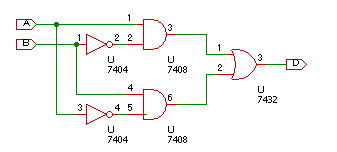
まとめとデモ
-
まとめ
論理和の否定は論理積になる(ド・モルガンの定理)
論理式は AND,OR,NOT 素子を組み合わせることで実現できる
n桁の2進数の加減算回路は、1桁の回路を並べて接続することで、実現できる。
2の補数を利用することで減算回路は、NOT回路と加算回路で実現できる。
-
デモ
1桁加算回路
3個のスイッチがA,B,Cに対応します。スイッチが押されると緑のランプが点灯します。加算した値が赤色のLEDで表示されます。
アンケート、課題
-
演習
■加算回路
3桁の加算回路のブロック図を描きなさい。
101 + 011 の計算を図の各出力に値を書き込みなさい。
-
課題
全加算器 桁上がりを計算する D の回路をスイッチ回路またはゲート回路で設計しなさい。
-
アンケート
■^((^A + B)・(A+ ^C))と等しいものはどれか(H21春 情報技術者試験)
1: A・^B + ^A・C 2:^A・B + ^A・C 3:(A+^B)・(^A+C) 4:(^A+B)・(A+^C)
■次の真理値表が表す論理式はどれか
1:(x ・ y)+z 2:(x+y)・z 3:x・(y+z) 4:x+(y・z)X Y Z 結果 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 1 1 1 0 1 1 1 1 1