逆理
数列に関するパラドックスに「ウサギと亀」の問題があります。
ウサギは亀の倍の速度で走ることができますが、ウサギが亀に追いつく間に亀は半分の距離を走ります。
したがって、「ウサギは亀に限りなく近づくことはできますが、追い抜くことはできない」が主張です。どこがおかしいのでしょうか？

数列とその和

１〜n の和
１からｎまでの和は、ちょっと工夫すると、簡単に計算できます。逆向きに展開した二つの数列を加えます。

Sn = 1 +  2 +  3        + (n-1) + n
Sn = n + (n-1)+(n-2)+   +    2  + 1

各項の和はすべて(n+1)になりますから、Snを次のように求めることができます。
　2Sn　= (n+1)*n

問題点
主張の問題点は「時間」にあります。最初に亀のいた位置(p)に追いつくまでの時間を t とします。この間に亀はp1まで移動します。亀はウサギの半分の速度ですから、ウサギがp1まで移動する時間は、t/2 となります。これをn回繰り返すと、
ウサギが亀に追いつくまでの時間の総和Tは
　T=ｔ（1 + 1/2 + 1/4 + 1/8 + ... 1/(2ⁿ)）
となります。これは r=1/2 の等比級数の和になります。nが十分大きいと(1/2)ⁿ=0ですから
　T=t（ rⁿ⁺¹-1）/(ｒ-１)=2ｔ
となります。2tはウサギが亀に追いつく時間で、これ以上時間は経過しないのです。

等差数列の和
隣り合う数の差が等しい数列を等差数列といいます。等差数列は一般に、a * n ＋b と表現できます。一般の等差数列の和も同じように計算できます。

図式解法
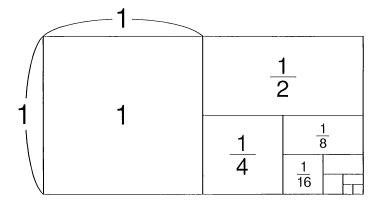
r = 1/2 の等比級数の和については、次のような図式解があります。

等比数列
隣り合う数の比が等しい数列を等比数列といいます。一般項は arⁿ となります。等比数列の和も面白い解法があります。等比数列Rnに対し、ｒ倍した数列rRnを考え、rRn - Rn を求めると、中間の項が消去されます。

Rn = 1+ r + r² + 　　　+ rⁿ
rRn = r + r² + 　　　+ rⁿ + rⁿ⁺¹

rRn-Rn = rⁿ⁺¹-1
これより、
Rn = （ rⁿ⁺¹-1）/(ｒ-１)

r = 2 の場合
r=2 の場合、等比級数の和はつぎのようになります。小さなnで確認してみてください。
1+ 2 + 2² + 　　　+ 2ⁿ= 2ⁿ⁺¹-1