微分方程式

微分方程式
接続した最初の時刻(t=0)ではコンデンサCに蓄積した電荷は0ですから、コンデンサCの両端の電圧は0です。したがって、流れる電流は　R/V　となります。
しかし、電流が流れると、コンデンサに電荷が蓄積され、それとともにコンデンサの両端の電圧が増加します。
　コンデンサの両端の電圧をv(t)とします。（(t)は時間のともに変換することを意味しています）。すると流れる電流は
　　V - v(t) = R・i(t)
となります。また、コンデンサに蓄積された電荷をq(t)とすると、
　q(t) = C・v(t)
の関係があります。また、i(t) = dq(t)/dt ですから、
　V - v(t) = RC ・dv(t)/dt
　RC ・dv(t)/dt + v(t) = V
となります。求めたい、v(t)に微分項がありますから、微分方程式とよびます、

解法
方程式を変形して
　dv(t)/dt =(1/RC)( -v(t) + V)
となります。これは（計数を除いて微分しても変化しない関数を意味します。この条件を満たす関数に指数関数があります。
　v(t)=a e^bt + k
として、方程式に代入します。
　ab e^bt =(1/RC)(-a e^bt - k+V)
この式が常に成立するには
　k=V
　ab = -a/(RC)
したがって　b=-1/(RC)
が必要です。これで、
　v(t)=a e^-1/(RC)t + V
となります。a は回路の初期条件から決定できます。時刻0でv(t)=0ですから、
　0= a + V
となります。したがって、a=-V
　v(t)=V(1- e^-1/(RC)t )
となります。

問題
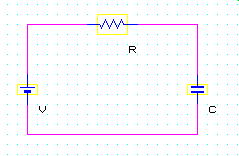
電圧VでコンデンサCを抵抗Rを通して充電する回路があります。時刻0でコンデンサの電荷が0として、充電を開始したばあい、時刻tのコンデンサの電圧を求めたい。

アプレット
この解を表示するアプレットです。コンデンサの容量はμファラッド、抵抗はΩです。電源の電圧は1.5Vです。
横軸は時間（秒）、縦軸は電圧です。