懸垂曲線
鎖や電線などが自重で垂れ下がった曲線を件垂線とよびます。昔は、放物線と考えられ、証明できませんでした。
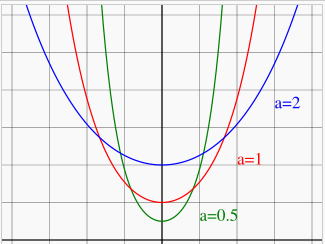
懸垂線は次の式で与えられます。
y = a (e x + e -x)
懸垂線は カテナリー曲線とも呼ばれます。
複利計算
年間100%の利息のサラ金業者がいるものとします。1年で100%ですから、
元金とあわせて(1+1)倍になります。
対数螺旋
極座標は、角度 θと原点からの長さ r で定義します。
r = e aθ
は対数螺旋と呼ばれます。角度θが一定量増加すると、長さ r は一定の比率で増加します。対数螺旋では、原点を通るすべての直線は、螺旋と等角度で交わることが証明されています。

a=1.08
半年、1/3年、1/n 年複利
これを半年複利にしますと、1年後には
(1 + 1/2)(1 + 1/2)=2.25 倍になります。4ヶ月複利では、3回繰り込みますから
(1+1/3) (1+1/3) (1+1/3) = 2.37倍です。
1月の複利ですと
(1 + 1/12)12 =2.613
1日では
(1 + 1/365)365 = 2.7145
になります。

e の級数表現
ex は微分しても同じ関数です。したがってマクローリン展開すると
、ex = 1 + (1/1!)x + (1/2!)x2 + (1/3!)x3
+ (1/n!)xn + ...
となります。ここで、x=1とすれば
、e = 1 + (1/1!) + (1/2!) + (1/3!) + (1/n!) + ...
となります。
極限
では、1/n 年複利でnを十分大きくすると、どうなるでしょう?
lim(1 + 1/n)n = 2.71828...
これは、e と表記されネピア数とか万有率とも呼ばれます。
自然対数の底としても利用されます。