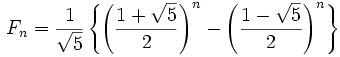フィボナッチ数と黄金比

定義
フィボナッチ数(Fibonacci number)は次にように再帰的に定義されます。
　Ｆ(1)＝Ｆ(2)＝１，
　Ｆ(n)＝Ｆ(n-1)＋Ｆ(n-2)　　ｎ≧３の時、

Fnの比
連続する Fn の数の比はnが大きいとき、
第2項の(1ー√5)/2 は１以下ですから、(1＋√5)/2 になります。

黄金比の長方形
黄金比の長方形で、短辺を辺とする正方形を取り除いてできる長方形は黄金比になります。

一般解

フィボナッチ数の一般解は次のように計算できます。

F(0)=0,F(1)=1;


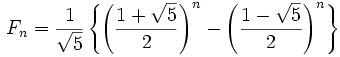
証明

数学的帰納法で証明します。
n乗される項を　a,b とします。このとき、a・b=-1、a+b=1、となります。
これを利用すると、以下のように証明出来ます。

f(k+1) = f(k) + f(k-1)
=(a^k-b^k)/√5 + (a^k-1 -b^k-1)/√5
=(a^k-b^k)/√5 +(-ba^k + ab^k)/√5 (ab=-1)
=((1-b)a^k - (1-a)b^k)/)/√5
=(a^k+1 -b^k+1)/√5（a+b=1)）

黄金比（golden ratio:分割）
黄金分割は二つの数の比として「美しい」比率といわれています。
これは、二つの数をa,b とすると
　a : b = b : (a + b)
を満たし、
　x² = x + 1
の解になります。
　この値は (1＋√5)/2 で、これはフィボナッチ数列 nが大きいときの Fn の比と同じです。

階段の昇り方　
n段の階段を1段、または、2段とびで昇る昇り方はフィボナッチ数になります。
　F（N)はF(n-1)に1段を加える、または、F(n-2)に2段を加えることになります。

//フィボナッチ数列の計算 
long Fib(int N) {
 long L; 
 //printf("in Fib(%d)\n",N);
 if (N==1 || N==2) return(1); 
 else { L=Fib(N-1)+Fib(N-2);
 //printf("return Fib(%d)=%ld\n",N,L);
 return(L); 
}