目的
スイッチ回路は論理式で表現できます。逆に言えば、任意の論理式の値はスイッチ回路で計算することができます。ここでは、論理式の性質や公式を紹介します。正確に言えば、すべての論理式が「そのまま」スイッチ回路計算できるわけではありませんが、適当な変形をすれば、スイッチ回路で計算することができます。
論理演算と論理式
-
論理演算を理解しよう
論理代数は値として0,1の二つの値のみをとる代数系で、・(論理積)、+(論理和)、^(論理否定)の三種の演算を持ちます。 ・ と + は二項演算、^ は単項演算であり、表1.1のように定義されます。演算子の優先順序は ^、 ・、+ の順とします。表のs先頭の行と列が演算される値で、表の中の値が演算した値です。
論理和は A または B どちらか一方(A or B)が1のとき、1 となりますから OR 演算、論理積は A と B (A and B)どちらも1なら結果は1となるから AND 演算ともよばれます。また、論理否定は逆(not)の値をとりますから NOT 演算ともよばれます。
論理和 論理積 否定 + 0 1 0 0 1 1 1 1 * 0 1 0 0 0 1 0 1 ^ 0 1 1 0
論理演算の例
演算は論理否定、論理積、論理和の順に行います。(..)があれば、その計算を優先します。
0 + 0 = 0, 0 + 1 = 1, 1 + 1 = 1
0・0 = 0, 0 ・ 1 = 0, 1 ・ 1 = 1
^0 = 1, ^1 = 0
1・0 + ^0・1 = 0 + 1・1 = 0 + 1 = 1
^(1・0 + 1) = ^1= 0
-
スイッチ回路との対応
0 と 1 をスイッチ(または回路)のオフとオンに対応させます。論理和は二つのスイッチの並列接続に対応します。いずれかのスイッチがオン(1)であれば、並列回路もオンになるからです。論理積は、二つのスイッチの直列接続に対応します。両方のスイッチがオン(1)であれば、直列回路もオンになるからです。
変数の論理否定はスイッチのオフ側(右下)の端子を利用します。スイッチがオフのとき、オフ側端子が左の端子と接続しています。スイッチがオンのときは、右上側の端子と左の端子が接続し、右下のオフ側の端子はオフとなります。
問題
次の計算をしなさい。( )がある場合、その値を先に計算します。
1 ・ ( ^0 + 0)=
^(0 + 1) ・ (0 + ^1) =
論理変数と論理式
-
論理変数とは
A,B,C..を0または1を表す論理変数とします。0との論理積は相手が0でも 1 でも 0 となりますから
A ・ 0 = 0
となります。同様に 0 と論理和しても値は変化しませんから
A + 0 = A
となります。
-
論理式
論理変数を演算すると論理式ができます。括弧がない場合、演算の順序は、否定、論理積、論理和の順とします。論理積は論理和に優先して演算されますから、
(A・B) + ((^C)・D) = A・B + ^C・D
と書くことができます。否定演算は論理積より優先します。
問題
各変数がとりうるすべての値の組に対し、次の論理式の値を求めなさい。
2変数の場合4通り、3変数の場合8通りあります。
^A・B + A・^B
A・B + ^A・B・C + C・^D
基本公式
論理式では定数と変数の間に次の性質があります。-
定数と変数
零元 A・0=0 A+0=A
単位元 A・1=A A+1=1
べき等律 A・A=A A+A=A
補元律 A・^A=0 A+(^A)=1
-
基本的性質
論理式では次の公式が成立します。
交換律 A・B=B・A A+B=B+A
結合律 A・(B・C)=(A・B)・C A+(B+C)=(A+B)+C
分配律 A・(B+C)=A・B+A・C A+(B・C) = (A+B)・(A+C)
ここで、( )は先に計算することを示します。(A+B)・(A+C) はA+B と A+C の論理積です。
-
分配律を回路で確認しよう
論理積の分配律の両辺を回路で表現すると、次のようになります。左右の回路が同じ機能であることを確認してください。
-
分配律の証明(しらみつぶし法で証明できる)
A・(B+C)=A・B+A・C を証明します。論理代数では、変数の取る値が限られていますからすべての場合を調べることで証明ができます。
完全しらみつぶし法による証明
A,B,Cはそれぞれ0と1しか値をとりませんから、すべての場合(4通り)を尽くせば証明になります。
部分的なしらみつぶしによる証明
各変数は0または1しか値をとりません。
A=0 の場合、左辺は0、右辺も0ですから成立します。
A=1 の場合、左辺は(B+C)で右辺もB+Cですから、この場合も成立します。
Aは0と1しか値をとりませんから、これで証明できたことになります。
問題 しらみつぶし法で次の式を証明しなさい。
A+(B・C) = (A+B)・(A+C)
ド・モルガンの定理
-
括弧式の否定は
^(A + B)のように、括弧のついた式の否定を含む式は、スイッチ回路では直接実現できません。直感的には
^(A + B) = ^A + ^B ------(これは誤り)
と考えがちですが、これは誤りです。例えば、Aを1、Bを0としたとき左辺は
^( 1 + 0 ) = 0
ですが、右辺は
^1 + ^0 = 0 + 1 = 1
となります。
論理式の最も重要な性質として、次のド・モルガン(De Morgan:人名)の定理を紹介します。否定のついた括弧をはずすには、このド・モルガンの定理を使います。
-
ド・モルガンの定理
論理代数で最も重要な定理を紹介します。
^(A・B) = ^ A+^B ^(A+B) = ^A・^B
[証明]
A=1 なら 左辺は ^B、右辺は 0 + ^B ですから成立します。
A=0 の場合、左辺は ^0 = 1、右辺は 1 + ^B = 1 となり、やはり、成立します。
-
論理和と論理積は表と裏の関係
ド・モルガンの定理は論理和と論理積が独立ではなく、論理和は論理否定と論理積から計算できることを意味します。すなわち、ド・モルガンの公式の両辺の 論理否定 をとると
^(^(A・B)) = A ・ B = ^(^A + ^B)
となります。したがって、各項の論理否定をとってから論理和し、その結果を論理否定をすれば、結果は論理積と同じになります。
例
ド・モルガンの定理を用いて括弧をはずします。
^(A・B +B・^C) = ^(A・B)・^(B・^C) = (^A + ^B)・(^B + C)
=^A .^B + ^A .C + ^B + ^B .C
最後の式は、スイッチ回路で実現できます。
問題
次の 二つ式の( )をはずして、展開しなさい。
~(A + B + C)=
^(A + B・^C)=
^((A +B ) ・ ^(A + C))=
^( C + D ・ ^E + F)=
論理式とスイッチ回路
-
論理式を計算するスイッチ回路
括弧の否定演算がなければ、論理式の値をスイッチ回路を使って計算できます。括弧の否定があっても、ドモルガンの公式で展開すれば、スイッチ回路で計算できます。
例
下の回路は (A+D)・(B+^C) の式の値を計算します。
スイッチ回路を設計する
ここで、回路の設計法を紹介します。まず、回路の入力と出力の対応表を作成します。これを真理値表と呼びます。真理値表は回路の仕様書になります。-
2変数の場合
- 真理値表
A,Bを入力として、次のようなXを出力する回路を設計します。これは、論理和とは異なり、排他的論理和(EXOR)と呼ばれる演算です。
A B X 0 0 0 0 1 1 1 0 1 1 1 0
- 設計
Xが1になるには、AがオフでBがオンである場合、あるいは、AがオンでBがオフの場合です。
これは、次のような論理式で表すことができます。
X = ^A・B + A・^B
この式を回路で表すと次のようになります。この回路は、Bのオン側とオフ側を逆にすると、先の階段スイッチと同じ回路になります。これは、「階段の点灯回路」と同じです。
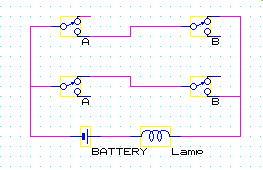
- 真理値表
-
3変数の場合
- 真理値表の例
次のような3変数の真理値表を例に考えます。この回路は、Cを桁上げとする AとB の桁上げ回路になります。
A B C | X
-----------
0 0 0 | 0
0 0 1 | 0
0 1 0 | 0
0 1 1 | 1
1 0 0 | 0
1 0 1 | 1
1 1 0 | 1
1 1 1 | 1
- 回路の合成
真理値表から、回路を作成することができます。
まず、出力が1になる場合を列挙して論理和します。上の例の場合4種類の入力に対してXが1になります。最初の条件は、C、Bが1で、Aが0の場合ですから、C・B・^Aとなります。他の場合も同様に合成すれば、
X=C・B・^A + C・^B・A + ^C・B・A + A・B・C
となります。このように、論理積された項を論理和した形式を加法標準形とよびます。この形式は関数が1となる場合をさがすのに便利です。これは
A+A=A の性質を利用して、A・B・C を付け加え
X=C・B・^A +A・B・C+ C・^B・A +A・B・C+ ^C・B・A + A・B・C
隣り合う項を、括弧でくくり
X=C・B・(A+^A)+A・C・(^B+B)+A・B・(^C+C)
A+^A=1 を利用すると
X=C・B +A・B+ C・A
となります。
- 真理値表の例
-
一般の場合
一般に、4,5変数の場合も、真理値から、同様に回路を導き出すことができます。基本的には、出力1を出す行をスイッチの直列回路で作成し、この行を並列に接続すれば、良いのです。この形式を「はしご型回路:ラダーサーキット」とも呼びます。
課題
以下の問題をレポート用紙にまとめ報告しなさい。- 問題
以下の式を計算する回路を設計しなさい。
^((A +B ) ・ ^(A + C))=
^( C + D ・ ^E + F)=
- 問題
次の真理値表を実現する論理式およびスイッチ回路を導きなさい。
A B C | X
-----------
0 0 0 | 0
0 0 1 | 0
0 1 0 | 0
0 1 1 | 1
1 0 0 | 0
1 0 1 | 1
1 1 0 | 1
1 1 1 | 1